Generacijos laikas

https://fineartamerica.com/featured/dividing-streptococcus-sp-bacterium-cnri.html

Skaičiuojant bakterijų generacijos laiką, darome prielaidą, kad jos dauginasi binarinio dalijimosi būdu, nes jis bakterijų atveju yra dažniausias. Kaip matote lentelėje, vienos ląstelės pasidalijimas sukuria dvi naujas ląsteles, dviejų ląstelių pasidalijimai sukuria keturias naujas ląsteles ir t.t. Kai ląstelių skaičius kiekvienoje kartoje (generacijoje) yra išreiškimas laipsniu, kurio pagrindas yra 2, laipsnio rodiklis nurodo įvykusių pasidalijimų (kartų) skaičių.

Laikas, reikalingas ląstelei pasidalinti (ir organizmų populiacijai padvigubėti) vadinamas generacijos laiku. Šis laikas varijuoja, priklausomai nuo konkrečių mikroorganizmų ir aplinkos sąlygų, pavyzdžiui, temperatūros, terpės. Daugumos bakterijų generacijos laikas yra apie 1-3 valandas, tačiau yra ir bakterijų, kurioms pasidalinti reikia daugiau nei 24 valandų. Pavyzdžiui, tinkamomis sąlygomis Streptococcus lactis generacijos laikas yra 30 min., Lactobacillus acidophilus 66-87 min., o Treponema pallidum 1980 min. (33 val.)

Jei binarinis bakterijų dauginimasis yra nesustabdomas, bus gautas milžiniškas ląstelių skaičius. Tarkime, kad dvigubėjimas vyksta kas 20 minučių (palankiomis sąlygomis per tokį laiką pasidalija E. coli), po 20 pasidalijimų iš vienos vienintelės ląstelės bus gauta daugiau nei milijonas ląstelių. Tai įvyktų per mažiau, nei 7 valandas. Po 30 pasidalijimų, arba 10 valandų, populiacijos dydis būtų milijardas ląstelių, o po 24 valandų ląstelių skaičių užrašytume skaičiumi, turinčiu 22 skaitmenis!

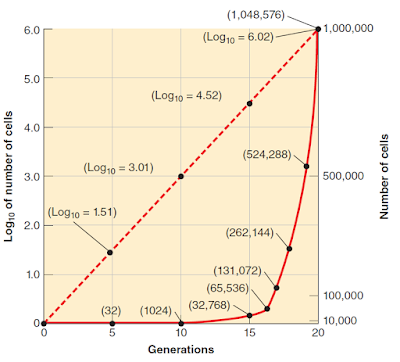
Jei naudotumėme aritmetinius skaičiavimus, būtų sudėtinga pavaizduoti tokios populiacijos augimą grafiškai, todėl populiacijų augimo kreivės įprastai vaizduojamos naudojant logaritmus. Kad geriau suprastumėm, kodėl vaizduojant augimo kreives, skaičiavimai keičiami į logaritminius, pavaizduokime 20 bakterijų pasidalijimų augimą. Po penkių (25) pasidalijimų iš vienos ląstelės gausime 32 ląsteles, po 10 (210) pasidalijimų 1024 ląstelių ir t.t. Gautus skaičius logaritmuojame (naudojamas dešimtainis logaritmas log10 arba lg), o gautas reikšmes pažymime grafike.

Matome, kad jei paliekame aritmetinį skaičiavimą, gaunama kreivė, kuri ne itin aiškiai parodo populiacijos kitimą ankstyvojoje stadijoje. Išvis atrodo, kad pirmuosius 10 pasidalijimų kreivė nepasikelia nuo x ašies. Taip pat toks braižymas nėra itin patogus, nes užima nemažai vietos lape.

Punktyrinė tiesė grafike parodo, kaip galima apeiti šiuos nepatogumus naudojant dešimtainį logaritmą (log10). Braižant tokį grafiką yra gaunama tiesė ir tolimesnių pasidalijimų skaičiaus logaritmai gali būti pažymėti neužimant daug papildomos vietos lape. Tačiau toks vaizdavimas iškreipia tikrąją situaciją populiacijoje (ji neauga tiesiškai, kaip vaizduoja kreivė), kadangi nesame įpratę galvoti logaritminėmis reikšmėmis, todėl mikrobiologai turi mokėti suprasti logaritmus ir jų skaičiavimus.

Deja, nuo kitos savaitės vėl prasideda mokslai, todėl blog'as grįš į seną tvarkaraštį - du įrašai per savaitę kiekvieną pirmadienį ir ketvirtadienį.

Iki kitų susitikimų :)

chekas

Informacijos šaltiniai:

• Gerard J. Tortora, Berdell R. Funke, Christine L. Case. “Microbiology. An Introduction”. 11th edition. p. 168-170
• http://www.biologydiscussion.com/bacteria/generation-time-of-bacteria-with-mathematical-expression/55137